문제 설명
테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈 공간에 적절히 올려놓으려 합니다. 게임 보드와 테이블은 모두 각 칸이 1x1 크기인 정사각 격자 모양입니다. 이때, 다음 규칙에 따라 테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈칸에 채우면 됩니다.
- 조각은 한 번에 하나씩 채워 넣습니다.
- 조각을 회전시킬 수 있습니다.
- 조각을 뒤집을 수는 없습니다.
- 게임 보드에 새로 채워 넣은 퍼즐 조각과 인접한 칸이 비어있으면 안 됩니다.
다음은 퍼즐 조각을 채우는 예시입니다.
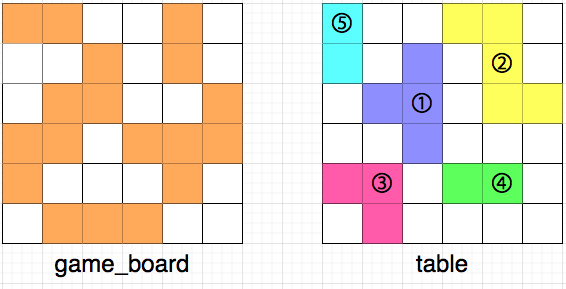
위 그림에서 왼쪽은 현재 게임 보드의 상태를, 오른쪽은 테이블 위에 놓인 퍼즐 조각들을 나타냅니다. 테이블 위에 놓인 퍼즐 조각들 또한 마찬가지로 [상,하,좌,우]로 인접해 붙어있는 경우는 없으며, 흰 칸은 퍼즐이 놓이지 않은 빈 공간을 나타냅니다. 모든 퍼즐 조각은 격자 칸에 딱 맞게 놓여있으며, 격자 칸을 벗어나거나, 걸쳐 있는 등 잘못 놓인 경우는 없습니다.
이때, 아래 그림과 같이 3,4,5번 조각을 격자 칸에 놓으면 규칙에 어긋나므로 불가능한 경우입니다.

- 3번 조각을 놓고 4번 조각을 놓기 전에 위쪽으로 인접한 칸에 빈칸이 생깁니다.
- 5번 조각의 양 옆으로 인접한 칸에 빈칸이 생깁니다.
다음은 규칙에 맞게 최대한 많은 조각을 게임 보드에 채워 넣은 모습입니다.

최대한 많은 조각을 채워 넣으면 총 14칸을 채울 수 있습니다.
현재 게임 보드의 상태 game_board, 테이블 위에 놓인 퍼즐 조각의 상태 table이 매개변수로 주어집니다. 규칙에 맞게 최대한 많은 퍼즐 조각을 채워 넣을 경우, 총 몇 칸을 채울 수 있는지 return 하도록 solution 함수를 완성해주세요.
제한사항
- 3 ≤ game_board의 행 길이 ≤ 50
- game_board의 각 열 길이 = game_board의 행 길이
- 즉, 게임 보드는 정사각 격자 모양입니다.
- game_board의 모든 원소는 0 또는 1입니다.
- 0은 빈칸, 1은 이미 채워진 칸을 나타냅니다.
- 퍼즐 조각이 놓일 빈칸은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
- table의 행 길이 = game_board의 행 길이
- table의 각 열 길이 = table의 행 길이
- 즉, 테이블은 game_board와 같은 크기의 정사각 격자 모양입니다.
- table의 모든 원소는 0 또는 1입니다.
- 0은 빈칸, 1은 조각이 놓인 칸을 나타냅니다.
- 퍼즐 조각은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
- game_board에는 반드시 하나 이상의 빈칸이 있습니다.
- table에는 반드시 하나 이상의 블록이 놓여 있습니다.
입출력 예game_boardtableresult
| [[1,1,0,0,1,0],[0,0,1,0,1,0],[0,1,1,0,0,1],[1,1,0,1,1,1],[1,0,0,0,1,0],[0,1,1,1,0,0]] | [[1,0,0,1,1,0],[1,0,1,0,1,0],[0,1,1,0,1,1],[0,0,1,0,0,0],[1,1,0,1,1,0],[0,1,0,0,0,0]] | 14 |
| [[0,0,0],[1,1,0],[1,1,1]] | [[1,1,1],[1,0,0],[0,0,0]] | 0 |
입출력 예 설명
입출력 예 #1
입력은 다음과 같은 형태이며, 문제의 예시와 같습니다.

입출력 예 #2
블록의 회전은 가능하지만, 뒤집을 수는 없습니다.
풀이
꽤 어려운 문제였다. 풀이의 큰 틀은 아래와 같다.
- table 를 돌면서 조각 칸을 발견.
- 발견한 조각 칸에 연결된 다른 조각 칸들 탐색.
- 조각 칸들을 묶은 블록 정보를 블록 리스트에 저장.
- game_board를 돌며 빈 칸을 발견.
- 발견한 빈 칸에 이어진 다른 빈 칸들 탐색하여 빈 칸 묶음 정보 도출.
- 빈 칸 묶음을 블록 리스트의 각 블록과 비교.
- 일치하면 game_board의 칸을 채우고 블록 리스트에서 해당 블록 삭제 및 answer 증가.
- 일치 안하면 game_board의 칸을 채운 후 다음 빈 칸 조사.
큰 틀은 생각하기 쉽다. 하지만 작은 기능들을 어떻게 구현해야 할지 꽤나 고민했다. 내가 한 고민거리와 그에 대한 답은 아래와 같다.
- 어떻게 이어진 칸들을 탐색할 것인가? : BFS든 DFS든 상관 없지만, 그냥 BFS로 했다.
- 이어진 칸들의 정보를 어떻게 블록으로 구조화 시킬 것인가? : 두 블록의 비교를 효율적으로 하기 위해 블록에 해당하는 칸들의 정보만을 vector로 저장했다. 블록 이외의 칸들은 저장하지 않았다.
- 블록의 영점을 어떻게 맞출 것인가? : 블록 데이터를 수집할 때, 각 블록들은 제각각의 위치에 있었고, 그 위치 정보를 토대로 블록 데이터를 구성했다. 때문에 블록 데이터들의 영점을 맞출 필요가 있었다. 블록의 좌표값들의 최소값이 무조건 0이 되도록 하는 작업이다. 이는 사실 구현하기 쉽다. 단순히 블록의 모든 칸들의 좌표값에서 일정 값(최소가 0이 되는 값)을 빼주면 된다.
- 블록 데이터의 순서는 어떻게 맞출 것인가? : 위의 영점 문제와 마찬가지로 각 블록들의 정보는 제각각의 회전형태로 수집되었기 때문에, 같은 모양의 블록정보를 같은 탐색 알고리즘으로 수집했다고 하더라도 각 칸들의 수집된 순서가 다를 수 있다. 따라서 수집된 칸 정보들을 정렬해주어서 순서를 맞췄다. 다행히 vector<pair<int,int>> 는 sort에 필요한 오버로딩이 이미 구현되어 있었기 때문에 단순히 sort함수만 호출해주면 자동 정렬된다.
- 두 블록을 어떻게 비교할 것인가? : 위에서 데이터의 순서 및 영점을 모두 맞췄고, 블록에 해당하는 칸들만 저장했기 때문에, 단순히 한 블록을 4방향으로 회전시켜가며 두 블록의 vector에 담긴 요소들이 모두 같은지만 확인하면 된다.
- 비교하려면 블록을 회전시켜야 하는데, 어떻게 할 것인가? : 회전의 경우 처음엔 어렵게 생각했다. 그러나 구글링을 통해 사실은 간단한 식 한 줄로 회전시킬 수 있다는 사실을 알았다. 회전된 칸의 좌표는 일정한 공식을 따른다. 그 공식은 아래와 같다.
B[ B Row ][ B Column ] = A[ N - B Column - 1 ][ B Row ]
출처 : https://taaewoo.tistory.com/10
시행착오
BFS로 블록의 칸들을 탐색했는데, 이 과정에서 큰 시행착오를 겪었다.
BFS 구현 시 방문할 칸이 저장된 큐에 이미 push된 칸을 또 큐에 push 하도록 구현한 것이다. 아래 코드를 보자.
Block BFSComposeBlock(vector<vector<int>>& table, int x, int y)
{
int findingV = table[x][y];
queue<pair<int, int>> q;
q.push({ x,y });
table[x][y] = 2;
Block block;
while (!q.empty())
{
pair<int, int> p(q.front());
q.pop();
//table[p.first][p.second] = 2; 문제코드
block.cells.push_back(p);
pair<int, int> p2;
for (int d = 0; d < 4; d++)
{
p2.first = p.first + DX[d];
p2.second = p.second + DY[d];
if (p2.first >= table.size() || p2.first < 0) continue;
if (p2.second >= table.size() || p2.second < 0) continue;
if (table[p2.first][p2.second] == findingV)
{
q.push(p2);
//table[p2.first][p2.second] = 2; 올바른 코드
}
}
}
block.SetZeroPosition();
return block;
}문제코드 라는 주석이 적힌 부분을 보자. 이미 방문한 칸을 표시하기 위해 2를 저장하고 있다. 그러나 저장하는 시점이 잘 못 됐다. 이렇게 구현할 경우 큐에서 pop한 칸에만 방문 표시가 되고, 이미 큐에 들어간 칸들은 방문표시가 안되어 있는 상황에 놓인다. 이 때 만약 큐에는 들어갔지만 방문표시가 안 된 칸 'A' 의 옆에 있는 칸이 pop될 경우, 칸 A가 또 다시 큐로 들어가게 될 수 있다. 만약 이해가 잘 안된다면 아래와 같은 블록 모양을 시뮬레이션 해 보면 이해가 더 잘 될 것이다.

따라서, 이 상황을 피하기 위해 칸이 큐에 삽입되는 시점에 방문표시를 해야한다.
코드
#include <string>
#include <vector>
#include <map>
#include <queue>
#include <iostream>
#include <algorithm>
using namespace std;
int DX[] = { -1,0,1,0 };
int DY[] = { 0,-1,0,1 };
int width;
class Block
{
public:
vector<pair<int, int>> cells;
void SetZeroPosition()
{
int minX = width, minY = width;
for (auto p : cells)
{
minX = min(p.first,minX);
minY = min(p.second, minY);
}
int leftMargin, upMargin;
if (minX > 0) leftMargin = minX;
else leftMargin = 0 - minX;
if (minY > 0) upMargin = minY;
else upMargin = 0 - minY;
for (auto& p : cells)
{
p.first -= leftMargin;
p.second -= upMargin;
}
sort(cells.begin(), cells.end());
}
void Rotate()
{
for (auto& p : cells)
{
pair<int, int> temp;
temp.first = width - p.second - 1;
temp.second = p.first;
p = temp;
}
}
static bool Compare(Block a, Block b)
{
if (a.cells.size() != b.cells.size()) return false;
int blockSize = a.cells.size();
for (int i = 0; i < 4; i++)
{
int match = 0;
for (int cellIdx = 0; cellIdx < blockSize; cellIdx++)
{
if (a.cells[cellIdx] != b.cells[cellIdx])
{
break;
}
match++;
}
if (match == blockSize)
{
return true;
}
b.Rotate();
b.SetZeroPosition();
}
return false;
}
};
map<int, Block> blockList;
Block BFSComposeBlock(vector<vector<int>>& table, int x, int y)
{
int findingV = table[x][y];
queue<pair<int, int>> q;
q.push({ x,y });
table[x][y] = 2;
Block block;
while (!q.empty())
{
pair<int, int> p(q.front());
q.pop();
block.cells.push_back(p);
pair<int, int> p2;
for (int d = 0; d < 4; d++)
{
p2.first = p.first + DX[d];
p2.second = p.second + DY[d];
if (p2.first >= table.size() || p2.first < 0) continue;
if (p2.second >= table.size() || p2.second < 0) continue;
if (table[p2.first][p2.second] == findingV)
{
q.push(p2);
table[p2.first][p2.second] = 2;
}
}
}
block.SetZeroPosition();
return block;
}
int solution(vector<vector<int>> game_board, vector<vector<int>> table) {
int answer = 0;
width = game_board.size();
int index = 0;
for (int i = 0; i < width; i++)
{
for (int j = 0; j < width; j++)
{
if (table[i][j] == 1)
{
Block b(BFSComposeBlock(table, i, j));
b.SetZeroPosition();
blockList[index++] = b;
}
}
}
for (int i = 0; i < width; i++)
{
for (int j = 0; j < width; j++)
{
if (game_board[i][j] == 0)
{
Block b = BFSComposeBlock(game_board, i, j);
b.SetZeroPosition();
for (auto block : blockList)
{
if (Block::Compare(block.second, b) == true)
{
blockList.erase(block.first);
answer += block.second.cells.size();
break;
}
}
}
}
}
return answer;
}'수학, 알고리즘' 카테고리의 다른 글
| [프로그래머스 Lv3] 섬 연결하기 (1) | 2022.10.03 |
|---|---|
| [프로그래머스 Lv3]퍼즐 조각 채우기 (2) | 2022.10.03 |
| [프로그래머스 Lv3. ]베스트앨범 (1) | 2022.09.21 |
| [프로그래머스 Lv3]단속카메라 (1) | 2022.09.17 |
| [프로그래머스 lv3]등굣길 (0) | 2022.09.12 |