문제 설명
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프들이 있습니다. 이 그래프들은 1개 이상의 정점과, 정점들을 연결하는 단방향 간선으로 이루어져 있습니다.
- 크기가 n인 도넛 모양 그래프는 n개의 정점과 n개의 간선이 있습니다. 도넛 모양 그래프의 아무 한 정점에서 출발해 이용한 적 없는 간선을 계속 따라가면 나머지 n-1개의 정점들을 한 번씩 방문한 뒤 원래 출발했던 정점으로 돌아오게 됩니다. 도넛 모양 그래프의 형태는 다음과 같습니다.
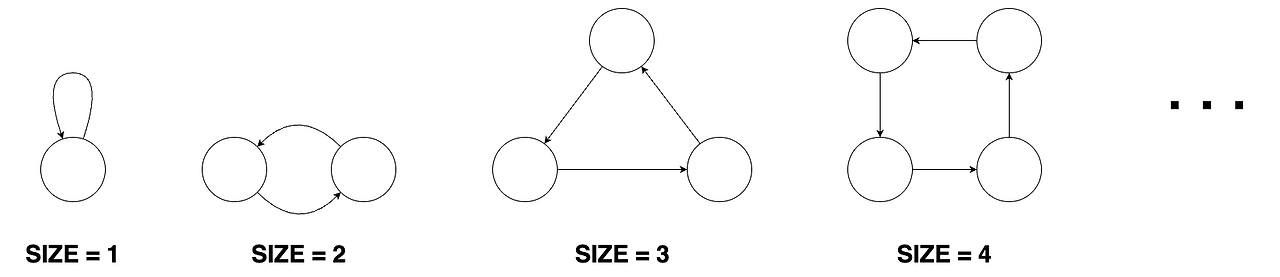
- 크기가 n인 막대 모양 그래프는 n개의 정점과 n-1개의 간선이 있습니다. 막대 모양 그래프는 임의의 한 정점에서 출발해 간선을 계속 따라가면 나머지 n-1개의 정점을 한 번씩 방문하게 되는 정점이 단 하나 존재합니다. 막대 모양 그래프의 형태는 다음과 같습니다.
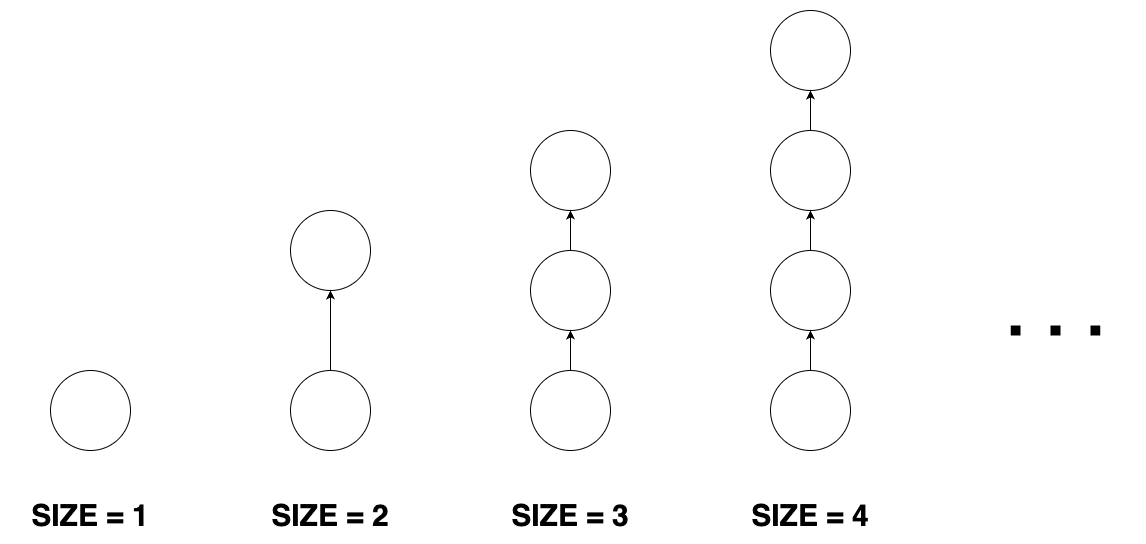
- 크기가 n인 8자 모양 그래프는 2n+1개의 정점과 2n+2개의 간선이 있습니다. 8자 모양 그래프는 크기가 동일한 2개의 도넛 모양 그래프에서 정점을 하나씩 골라 결합시킨 형태의 그래프입니다. 8자 모양 그래프의 형태는 다음과 같습니다.
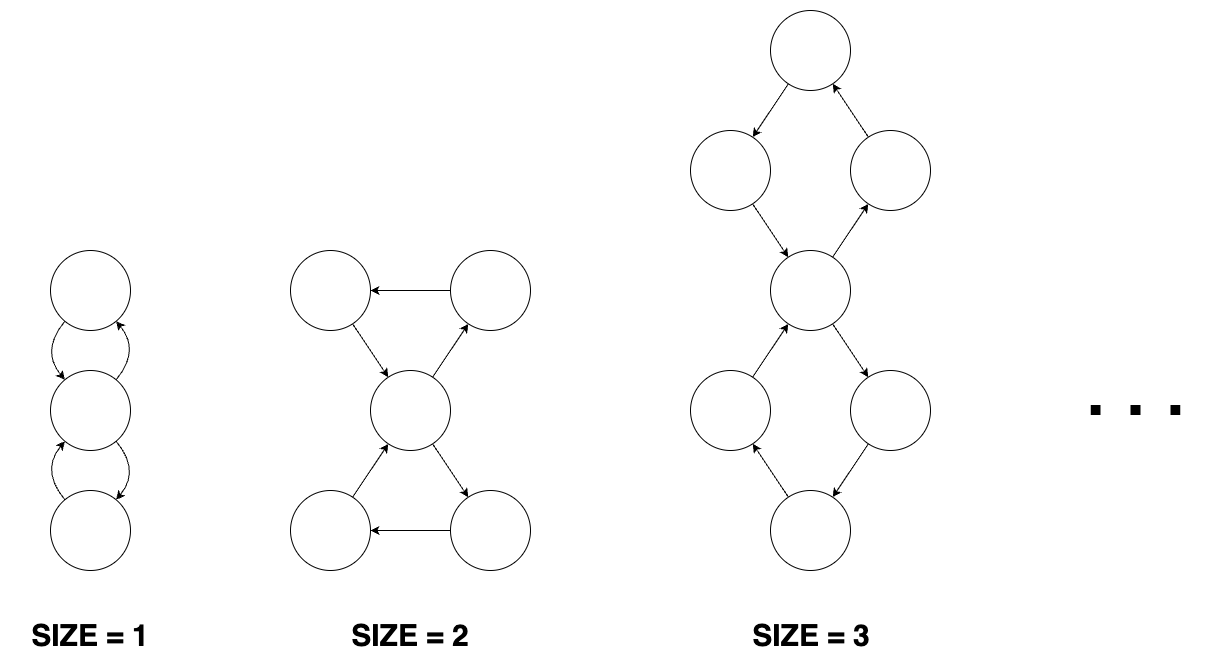
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프가 여러 개 있습니다. 이 그래프들과 무관한 정점을 하나 생성한 뒤, 각 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 임의의 정점 하나로 향하는 간선들을 연결했습니다.
그 후 각 정점에 서로 다른 번호를 매겼습니다.
이때 당신은 그래프의 간선 정보가 주어지면 생성한 정점의 번호와 정점을 생성하기 전 도넛 모양 그래프의 수, 막대 모양 그래프의 수, 8자 모양 그래프의 수를 구해야 합니다.
그래프의 간선 정보를 담은 2차원 정수 배열 edges가 매개변수로 주어집니다. 이때, 생성한 정점의 번호, 도넛 모양 그래프의 수, 막대 모양 그래프의 수, 8자 모양 그래프의 수를 순서대로 1차원 정수 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
제한사항
- 1 ≤ edges의 길이 ≤ 1,000,000
- edges의 원소는 [a,b] 형태이며, a번 정점에서 b번 정점으로 향하는 간선이 있다는 것을 나타냅니다.
- 1 ≤ a, b ≤ 1,000,000
- 문제의 조건에 맞는 그래프가 주어집니다.
- 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 수의 합은 2이상입니다.
입출력 예edgesresult
| [[2, 3], [4, 3], [1, 1], [2, 1]] | [2, 1, 1, 0] |
| [[4, 11], [1, 12], [8, 3], [12, 7], [4, 2], [7, 11], [4, 8], [9, 6], [10, 11], [6, 10], [3, 5], [11, 1], [5, 3], [11, 9], [3, 8]] | [4, 0, 1, 2] |
입출력 예 설명
입출력 예 #1
주어진 그래프를 그림으로 나타내면 다음과 같습니다.
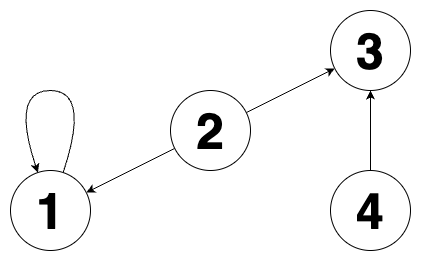
2번 정점이 생성한 정점이고 도넛 모양 그래프 1개, 막대 모양 그래프 1개가 존재합니다. 따라서 [2, 1, 1, 0]을 return 해야 합니다.
입출력 예 #2
주어진 그래프를 그림으로 나타내면 다음과 같습니다.
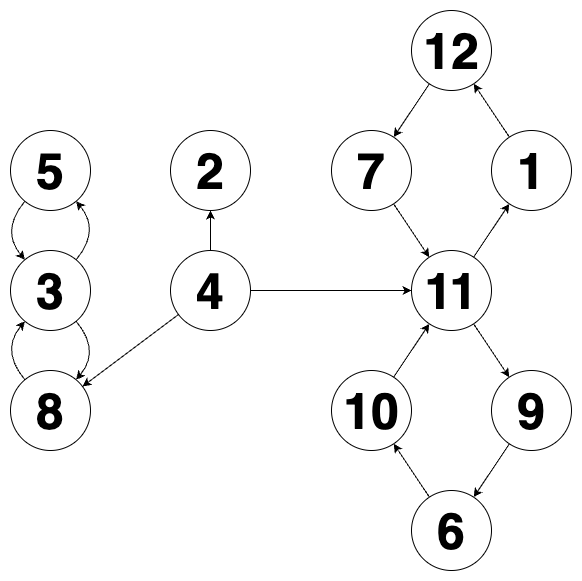
4번 정점이 생성한 정점이고 막대 모양 그래프 1개, 8자 모양 그래프 2개가 존재합니다. 따라서 [4, 0, 1, 2]를 return 해야 합니다.
풀이
각 그래프마다 1개의 점과 중점은 저마다의 특징이 있는데, 이를 잘 파악하는 것이 핵심이다.
이 특징을 파악하고 나면, 단순히 모든 정점을 순회하며 특징과 일치하는지 검사하면 된다.
특징은 아래와 같다.
중점(생성된 점) : 들어오는 간선은 0개, 나가는 간선이 2개 이상이다.
도넛 그래프 : 들어오는 간선 1개 이상, 나가는 간선이 1개 있다.
막대 그래프 : 끝 점의 나가는 간선이 0개다.
8자 그래프 : 중심점의 들어오는 간선이 2개 이상, 나가는 간선이 2개 있다.
그런데 위의 특징 만으로는 도넛 그래프의 갯수를 파악하는 데에 문제가 있다. 도넛 그래프는 모든 정점이 똑같이 생겼고, 심지어 8자 그래프의 중점을 제외한 나머지 정점과도 똑같이 생겼다. 따라서 모든 점을 순회하며 도넛 그래프의 특정 점을 조사해서 도넛 그래프의 정점인지 알 수 없다.
하지만 중점에 연결된 간선의 갯수는 곧 모든 그래프의 갯수와 같고, 도넛을 제외한 나머지 그래프들의 갯수를 알 수 있으므로,
도넛 그래프의 갯수 = 모든 그래프의 갯수 - 도넛 제외 나머지 그래프의 갯수
의 계산으로 도넛 그래프의 갯수를 알 수 있다.
코드
#include <string>
#include <vector>
#include <map>
#include <iostream>
using namespace std;
map<int,vector<int>> edgesOut;
map<int,vector<int>> edgesIn;
int iEdgeCount = 0;
int iVertexCount = 0;
int iGraphCount = 0;
//막대 : 나가는 게 없는 애가 1개 있음.
//8 : 들어오는 거 2개 이상, 나가는 거 2개
//중점 : 들어오는거 0개, 나가는 거 2개 이상
//도넛 : 중점에 연결된 정점의 갯수 - 나머지 그래프 갯수.
vector<int> solution(vector<vector<int>> edges) {
vector<int> answer(4);
iEdgeCount = edges.size();
for(auto i : edges)
{
edgesOut.insert({i[0]-1,vector<int>()});
edgesIn.insert({i[0]-1,vector<int>()});
edgesOut.insert({i[1]-1,vector<int>()});
edgesIn.insert({i[1]-1,vector<int>()});
edgesOut[i[0]-1].push_back(i[1]-1);
edgesIn[i[1]-1].push_back(i[0]-1);
iVertexCount = max(i[0], iVertexCount);
iVertexCount = max(i[1], iVertexCount);
}
for(auto i : edgesOut)
{
int iVertex = i.first;
int iOutCount = edgesOut[iVertex].size();
int iInCount = edgesIn[iVertex].size();
//cout << "vertex:"<<iVertex+1 <<", outC:"<<iOutCount<<", inC:"<<iInCount;
//중점
if(iOutCount >=2 && iInCount == 0)
{
//cout <<"/ center"<<endl;
answer[0] = iVertex+1;
iGraphCount = iOutCount;
continue;
}
//8자
if(iOutCount ==2 && iInCount >= 2)
{
//cout <<"/ eight"<<endl;
answer[3]++;
continue;
}
//막대
if(iOutCount == 0 )
{
//cout <<"/ stick"<<endl;
answer[2]++;
continue;
}
// cout <<"/ noting or dough"<<endl;
}
answer[1] = iGraphCount;
answer[1] -= answer[2];
answer[1] -= answer[3];
return answer;
}'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준] 14503 로봇청소기 (0) | 2025.05.03 |
|---|---|
| [프로그래머스 Lv3]산 모양 타일링 (0) | 2024.07.09 |
| [백준] 1060 좋은 수 (0) | 2024.05.04 |
| [백준]1285 동전 뒤집기 (1) | 2024.04.26 |
| [백준]1525 퍼즐 (0) | 2024.04.23 |