문제
https://www.acmicpc.net/problem/1167
1167번: 트리의 지름
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지
www.acmicpc.net
풀이
무엇보다 트리의 특성을 잘 이용하는 것이 중요한 문제입니다.
트리는 두 점 사이의 경로가 단 1개입니다. 따라서 가장 멀리 떨어진 두 점 (a, b)사이의 길이가 트리의 지름이 됩니다.
그렇다면 문제는 가장 멀리 떨어진 두 점 a와 b를 어떻게 찾을 것인가? 를 고민해야 합니다.
아래는 제가 맘대로 만든 트리입니다. 각 노드에는 번호가 적혀있고, 연결한 선분에는 길이가 적혀있습니다.
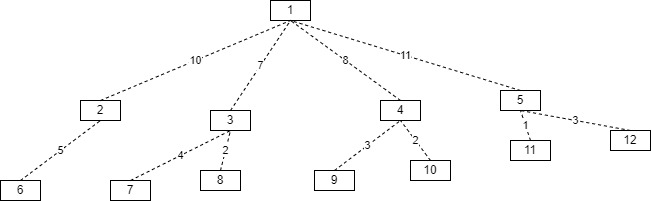
위 그림은 일반적인 트리의 모습입니다. 각 노드 사이의 거리가 다릅니다.
정답먼저 말하자면, 노드 사이의 길이가 가장 긴 점들은 경로의 길이가 29인 6, 12 입니다. 즉, 위에 말했던 a,b가 6,12입니다.
그럼 일단 a,b가 뭔지 모른다고 치고, 우선 a, b중 하나를 찾기 위해 아무 노드(v)를 선택해서 v로부터 가장 먼 노드를 계산해봅시다.
v가 1이라고 했을 때, 가장 먼 노드는 경로의 길이가 15인 6입니다.
v가 8이라고 했을 때, 가장 먼 노드는 경로의 길이가 24인 6입니다.
v가 2라고 했을 떄, 가장 먼 노드는 경로의 길이가 24인 12입니다.
v가 4라고 했을 때, 가장 먼 노드는 경로의 길이가 26인 6입니다.
...
공교롭게도 v와 가장 먼 노드들이 전부 지름의 양 끝단인 6, 12중 하나입니다.
이것은 우연일까요?
아뇨. 트리의 특성 상 이렇게 될 수 밖에 없습니다.
임의의 노드(v)로부터 거리가 가장 먼 노드(u)까지의 경로들이 공통적으로 지나는 노드(t)가 반드시 1개는 존재합니다.(자세한 내용은 아래 참고)
위의 예에서는 루트노드인 1이 t가 되겠네요. (꼭 루트노드가 t인건 아닙니다)
그리고 t로부터 거리가 가장 먼 노드는 변하지 않죠. 바로 양 끝단에 위치한 a혹은 b입니다.
즉, 경로(v -> u)는 항상 t를 지나기 때문에 (v -> u) = (v -> t) + (t -> u) 가 되고, (t -> u) 가 가장 길어지는 u는 a혹은 b일 수 밖에 없다는 것입니다.
이해가 어렵다면, 이렇게 생각할 수도 있습니다.
원 안에서 아무 점(v)이나 찍어봅니다. 그리고 v에서 가장 먼 원 안의 점(u)을 찍어봅니다. u는 자연스럽게 원의 가장 끝에 찍힙니다. 즉, u는 원을 이루는 선 위의 점(a 혹은 b)입니다. 그리고 v와 u를 잇는 선분은 반드시 원의 중심(t)를 지납니다.
이것을 트리에도 똑같이 적용할 수 있습니다.
아래 그림은 트리를 원 모양으로 만든 것입니다. 6, 12번 노드가 지름이라서 일직선으로 놓아보았습니다.
또한 각 노드를 연결하는 선의 길이는 대강 노드 사이의 길이랑 맞춰보았습니다.

여기서 아무 노드나 골라서 그 노드와 가장 거리가 먼 노드를 찾아보면, 원의 선 위에 위치한 6, 12 둘 중 하나일 것이라는 걸 알 수 있습니다.
그렇다면 경로 (a->b)의 길이를 구하기 위해서는 아무 노드(v)를 시작으로 DFS를 활용해 거리가 가장 먼 노드(a)를 찾아준 뒤,
다시 DFS를 활용해 a에서 거리가 가장 먼 노드(b)까지의 거리를 구해주면 되겠네요.
와~ 풀이 끝~
참고
위의 풀이에서 다음과 같은 말을 했습니다.
임의의 노드(v)로부터 거리가 가장 먼 노드(u)까지의 경로들이 공통적으로 지나는 노드(t) 가 반드시 1개는 존재합니다.
그런데 이거 진짜일까요? t가 없을 수도 있지 않을까요?
트리라는 것은 임의의 노드는 반드시 모든 다른 노드들과 연결되어 있어야 하고, 그 경로는 한가지여야 합니다.
6과 12는 지름이므로 원의 선 위에 존재하고, 서로간의 거리가 가장 멉니다.
그리고 6과 12의 사이에는 2, 1, 5가 존재합니다.
그런데, 만약 6, 12 두 개의 노드로만 구성된 트리가 아닌 이상, 6과 12사이에 아무 노드도 없을 수 있을까요?
그럴 수 없습니다. 왜냐하면 트리의 모든 노드는 연결되어야 하는데, 다른 노드들이 연결될 노드(t)가 없으니까요.
t가 없다고 나머지 노드들이 6이나 12에 연결될 수도 없습니다.
만약 다른 노드들이 6 혹은 12에 연결되어 있다면 더이상 6과 12가 지름의 양 끝단 노드가 아닐 것입니다. 그보다 더 긴 길이의 경로가 생겼으니까요.
그러므로 6과 12 사이에는 반드시 하나 이상의 노드가 존재해야합니다.
그리고 그 노드에는 다른 노드들이 연결되고, 그 노드에서 거리가 가장 먼 노드는 반드시 t의 반대편에 존재하므로, t를 거쳐갈 수 밖에 없습니다.
따라서 a와 b사이에는 반드시 하나 이상의 노드(t)가 존재해야 하고, 그 노드는 임의의 노드(v)로부터 거리가 가장 먼 노드(u)까지의 경로들이 공통적으로 지나는 노드입니다.
코드
// CodeTest.cpp : 이 파일에는 'main' 함수가 포함됩니다. 거기서 프로그램 실행이 시작되고 종료됩니다.
//
#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
using namespace std;
int V;
map<int, vector<pair<int,int>>> Map;
vector<bool> isVisited;
int point;
int dist =0;
void PrintMap()
{
for (auto& i : Map)
{
cout << i.first << " ";
for (auto& j : i.second)
{
cout << "<" << j.first << "," << j.second << ">";
}
cout << endl;
}
}
pair<int,int> DFS(int current, int distFromStart)
{
pair<int, int> ret = { current,distFromStart };
isVisited[current] = true;
for (auto& i : Map[current])
{
if (isVisited[i.first] == true)
continue;
pair<int, int> tmp = DFS(i.first, distFromStart + i.second);
if (tmp.second > ret.second)
ret = tmp;
}
return ret ;
}
int main()
{
cin >> V;
for (size_t i = 0; i < V; i++)
{
int vertex, vertex2, dist;
cin >> vertex;
while (true)
{
cin >> vertex2;
if (vertex2 == -1)
break;
cin >> dist;
Map[vertex-1].push_back({vertex2-1, dist});
}
}
isVisited.resize(V, false);
pair<int,int> point = DFS(0,0);
fill(isVisited.begin(), isVisited.end(), false);
point = DFS(point.first,0);
cout << point.second;
}
'수학, 알고리즘' 카테고리의 다른 글
| [백준]1285 동전 뒤집기 (1) | 2024.04.26 |
|---|---|
| [백준]1525 퍼즐 (0) | 2024.04.23 |
| [프로그래머스 lv 2] [PCCP 기출문제] 2번 / 석유 시추 (0) | 2024.02.22 |
| [프로그래머스 Lv3] 인사고과 (0) | 2023.08.24 |
| [프로그래머스 lv3] 미로 탈출 명령어 (1) | 2023.05.30 |